Un ente privo di dimensioni, ma fondamentale

In matematica, il punto è un ente geometrico fondamentale, il primo mattone di uno straordinario edificio. Proviamo allora a raccontare l’evoluzione di questo concetto a partire dalle sue origini.

La geometria che tutti conosciamo e che è stata formalizzata da Euclide, matematico greco vissuto tra il IV e il III secolo a.C., definisce, cioè descrive tutti i suoi oggetti (i suoi “enti”) facendo riferimento ad altri enti già noti. Così un quadrato è “un poligono con quattro lati uguali e quattro angoli uguali”, poiché già sono stati definiti i concetti di poligono, di lato, di angolo e di uguaglianza. Procedendo così a ritroso, arriviamo ai primi enti, quelli che fanno da base a tutta questa costruzione e che quindi non possono essere definiti. Per Euclide, questi enti fondamentali sono il punto, la retta e il piano. Essi sono unicamente descritti in modo che lo studente possa intuirne un’idea.

Così per Euclide il punto è “ciò che non ha parti”; potremmo anche dire che è ciò che non ha dimensioni, quindi né lunghezza né larghezza né profondità. È un’astrazione, un oggetto ideale: non esistono nella realtà oggetti privi di dimensioni! Anche il più minuscolo segno di penna su un foglio ha una larghezza e una lunghezza e, a essere precisi, anche uno spessore. E così un granello di sabbia o un atomo hanno dimensioni che possono essere misurate.

Il punto è anche l’unità fondamentale che permette di costruire gli altri enti geometrici: una retta e un piano sono formati da punti opportunamente disposti. Questi enti fondamentali sono protagonisti dei postulati che Euclide pone a fondamento del suo trattato di geometria, “Gli elementi”. I postulati sono le proposizioni assunte come vere e dalle quali discendono per dimostrazione tutte le altre proposizioni, i teoremi.

Il punto è poi il protagonista di due dei postulati di Euclide: il primo afferma che due punti possono essere sempre congiunti da una linea retta; il terzo che un punto e una lunghezza determinano un cerchio di cui il punto è il centro e la lunghezza il raggio.

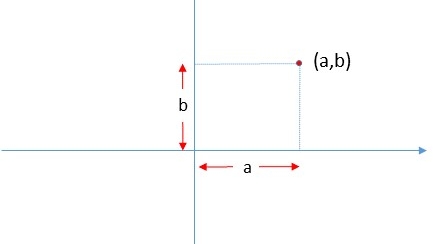
Nell’astrazione matematica un punto, non avendo dimensioni, è identificato solo dalla sua posizione: a sinistra o a destra di una retta, sopra o sotto un piano, allineato ad altri punti... René Descartes, filosofo e matematico francese vissuto nel XVII secolo, inventò un metodo per precisare in modo quantitativo queste informazioni sulla posizione dei punti: legando la geometria all’algebra introdusse un “sistema di riferimento”, quello che conosciamo come “piano cartesiano”: fissate due rette perpendicolari, la posizione di ogni punto del piano è determinata da due numeri, che esprimono la sua distanza da queste rette. Quindi, con l’introduzione dei sistemi di coordinate, la posizione di un punto è determinata in modo unico da un numero (se si trova su una fissata linea), da due numeri (se si trova in un piano) o più in generale da n numeri se si trova in uno spazio a n dimensioni.

Ma quanti punti ci sono su una retta? Infiniti, certo. Ma quanti? Più che in un segmento? L’occhio ci direbbe di sì. Invece in ogni segmento o retta il numero di punti è lo stesso. Per essere più chiari e precisi, se consideriamo due segmenti qualsiasi, anche di lunghezza diversa, i loro punti possono essere messi in corrispondenza biunivoca (cioè a ogni punto del primo corrisponde un punto del secondo e viceversa) e quindi i due segmenti hanno lo stesso numero di punti. Paradossi che ci sorprendono quando cerchiamo di pensare l’infinito.

E, a proposito di infinito, per i matematici ogni retta ha un “punto all’infinito”: nella geometria proiettiva, nata nel XVII secolo come tentativo di formalizzazione del disegno prospettico e poi sviluppatasi nel XIX secolo, due rette si incontrano sempre in un punto. Se le rette sono parallele, il loro punto comune si trova all’infinito.      

Anche la fisica, che è legata al mondo materiale più della matematica, ricorre al concetto di “punto materiale” come approssimazione: si tratta di un oggetto senza dimensioni, ma comunque dotato di una massa e/o di una carica elettrica. Assurdo, vero? Eppure, è un’utile semplificazione quando le dimensioni del corpo che stiamo studiando sono molto piccole rispetto alle distanze considerate. Così un proiettile lanciato da un fucile, un piccolo oggetto lasciato cadere da una grande altezza possono, in prima approssimazione, essere trattati come punti pesanti in modo da semplificare la descrizione del loro moto.

Fonte: Francesca Carfora, Istituto per le applicazioni del calcolo “Mario Picone”, f.carfora@na.iac.cnr.it